Using Bayesian Models to make Business Decisions
March 10th, 2021 by Lorre
There are various fields that have data, which can be used to make informed business decisions. Supply chain is one example of an exciting area, where retailers, shipping companies or any organization with supply and demand data can utilize machine learning (ML) to increase their margin profits through prediction. There are two ways to approaching ML (and statistics): the frequentist approach, which is more common, and the Bayesian approach, the less well-understood counterpart. Frequentist statistics bases its probabilities on counts of occurrences, while Bayesian assumes that probabilities are derived from Bayes Rule.
Bayesian vs Frequentist Models
- Parameters are unknown and random vs fixed
- Parameters have distributions of values reflecting uncertainty vs one true value
- Credible intervals (95% probability that the population value is within limits of the interval) vs confidence intervals
Bayesian Lingo
Bayes Rule states (in essence):
Pr(cause | effect) = [Pr(effect | cause) x Pr(cause)] / Pr(effect)
Essentially, Bayes rule gets distilled to:
Pr(cause | effect) proportional to [Pr(effect | cause) x Pr(cause)]
because the probability of the effect (or the Marginal) needs to integrates to 1 to be a valid probability distribution, which it great as it requires exact inference (typically a hard integration problem).
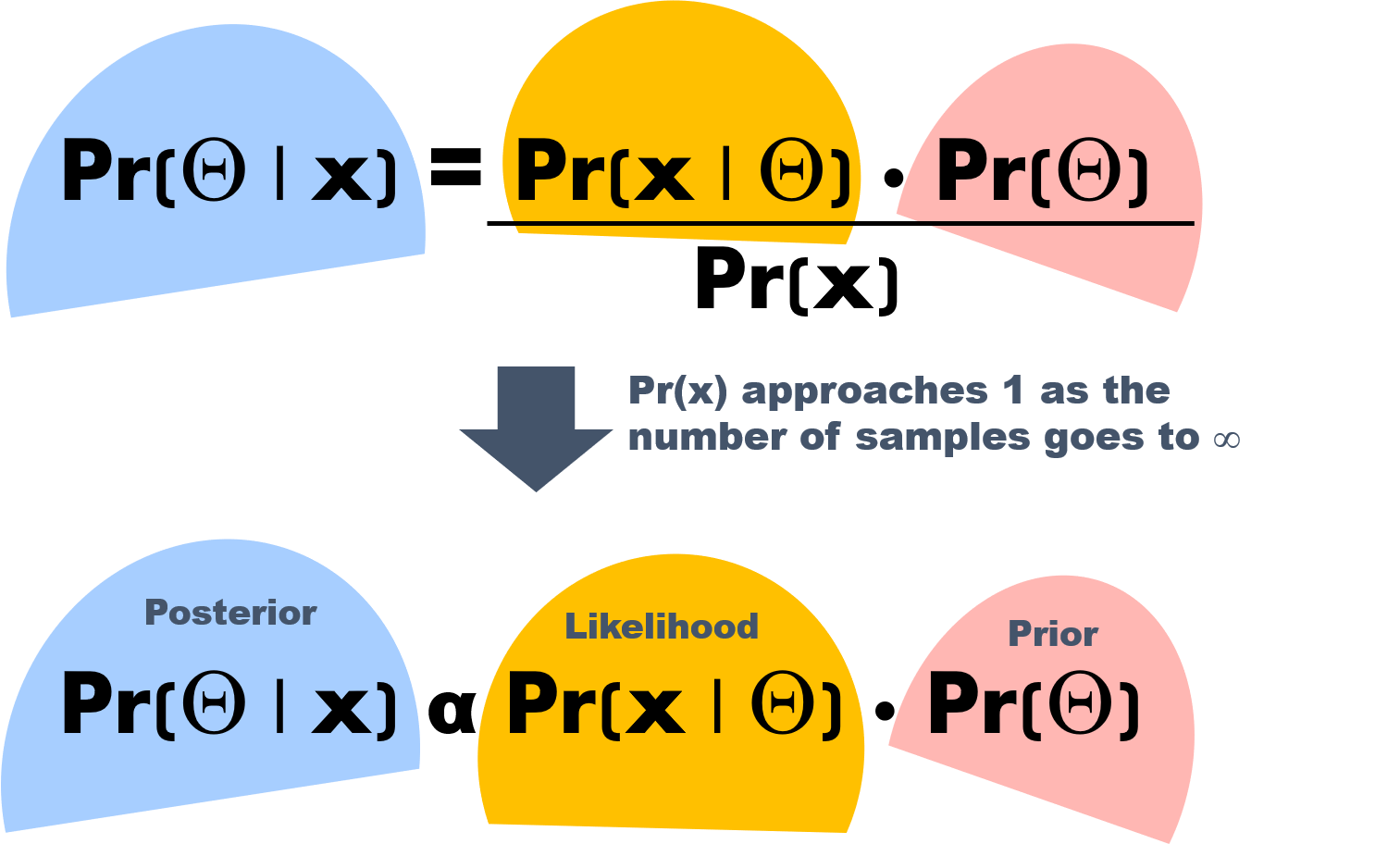
Posterior
The probability of finding the cause given effect is what we want to find. It can also be thought of as the probability of finding model parameters that explain some phenomena in the data, x.
Likelihood
The probability of the effect given the cause or the probability that data, x occurs given model parameters.
Prior
This specifies probability of the cause or the distribution of model parameters (coefficients).This will characterize the behavior of the likelihood.
Why take the Bayesian Approach?
Good for Small to Medium Datasets
Bayesian models are particularly powerful in the case of small-ish datasets as we can eliminate directly computation of the marginal distribution by drawing samples from the dataset. With Frequentist models, having fewer observations than features can severely limit its predictive capability and usage. As for all models, more data is generally better, however Bayesian models may find it easier to hit that sweet spot among data quality/quantity and predictive power.
Includes Your Prior Knowledge
Bayesian models allow designation of priors, which are permit users to embed domain expertise about how the model should work. For example, let’s say we are predicting the probability of making more than $50k as a function of age, years of education and hours worked per week. We have the option of using sociological knowledge about the effects of age and education on income by specifying a prior, where a Normal distribution about mean of 1 for education would imply that we believe that on average increases in the number of years of education will positively affect income. Alternatively, specifying a prior for hours as a Normal distribution with mean -2 implies that the higher the number of hours worked, the lower the income (on half the scale). Often, we as modelers know quite a bit a bit about the behavior of the data that we are working with and can include priors to provide significant insight into the overall behavior of the model.
Quantify Uncertainty of Results
While Maximum Likelihood Estimation (MLE) (taking a frequentist approach) returns a single parameter estimate, Maximum a Posteriori (MAP) provides a distribution over parameter values, which lends itself well to quantifying certainty of that parameter.
How to use Bayesian Models for Business Decisions
1. Explore your dataset
Clean and transform (e.g. normalize features) the data so that you are familiar with any issues or limits of using the data for modeling.
2. Select & Fit Bayesian Model
We could fit the data to a simple approximation such as a Poisson distribution or more complex generalized hierarchical linear model depending on the nature of your use case and the availability of data. This allows the modeler to directly assess uncertainty of the model parameters and to generate posterior predictive samples that can be used to train or test out new hypotheses, which is particularly helpful for optimizations.
3. Analyze the Results
We can explore the fit of our model and evaluate the suitability of the selected priors and likelihood to ensure we have a useful model. We can also explore the relationships between model parameters, which is helpful when we have several features to consider at once.
4. Optimization of Bayesian Model
We can gain real insight into our ML problem and make practical business decisions by optimizing over supply and demand signals.
Considerations Before Going Bayesian
Choosing The Likelihood
Think about the behavior that the model is trying to explain when selecting the Likelihood. You should find the likelihood that suits the data e.g. selecting the Poisson distribution when describing counts of discrete events that occur independently. Check out the distribution zoo to explore all of the various options!
Choosing the Prior
Keep in mind that some parameters are bounded between 0 and 1, so be sure to account for when selecting a prior otherwise your models wont make sense. Distribution zoo will also come in handy here. We can also choose a weakly informative prior if we are ignorant of the true values of the model parameters.
In summary, being familiar with the data and model that you are trying to fit will greatly inform your choice of likelihood and prior. Without good priors and likelihoods, your model may be poor.
For more examples of Bayesian models coded in Python, check out my supply chain repo.