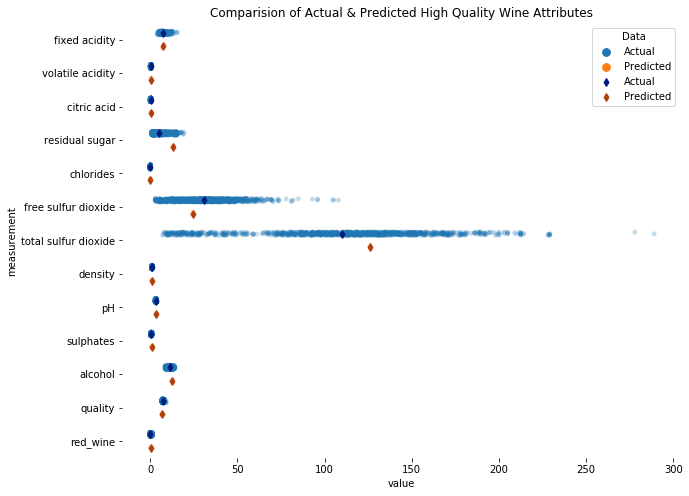
There are various approaches that one can take to reverse-engineer a trained machine learning model and we explore this problem by implementing simulated annealing (SA). SA is often used for problems with discrete search spaces e.g. job scheduling or the traveling salesman problem. It may be used for hard optimization problems where exact algorithms fail and the gradient is unknown, but the approximate global solution is good enough. To better understand SA, we will implement this algorithm to optimize over Portuguese wine characteristics, like acidity and pH, to find the best quality wine.

The Dataset

For this analysis, we will combine two datasets containing numeric attributes describing both red and white variants of the Portuguese “Vinho Verde” wine.

The input variables (based on physicochemical tests):

1. fixed acidity

2. volatile acidity

3. citric acid

4. residual sugar

5. chlorides

6. free sulfur dioxide

7. total sulfur dioxide

8. density

9. pH

10. sulphates

11. alcohol

The output variable (based on sensory data):

1. quality (score between 0 and 10)

For more details, consult the reference

Introduction to Simulated Annealing

SA is a gradient-free optimization technique used when the space has lots of local minima to get stuck in. It is probabilistic (meaning it depends on some randomness as opposed to generating the same answer every time) and finds the approximate global optimum of a given function. Due the randomness, it may be a good idea to run the SA algorithm multiple times to ensure consensus on finding the global optimum. Just like any other optimization technique, SA requires input variables (typically many variables that define the search space and which may be subject to constraints), and an objective or cost function (function that measures whether a solution is good or bad).

Its name comes from annealing or heating and controlled cooling of metal to alter its physical and/or chemical properties. Changes to a material’s temperature affect its thermodynamic free energy. SA works by simulating cooling i.e. lowering of temperature as the search space is explored. At each temperature step, SA randomly selects a neighboring solution to the current solution and measures its cost according to the objective function and will accept or reject the neighboring solution, depending on its temperature. At higher temperatures, SA is more likely to accept worse solutions as the solution space is explored, while SA tends to exploit the solution space at lower temperatures.

Approach

1. Train regression model (via xgboost) to predict quality of wine based on physiochemical properties

2. Apply simulated annealing optimize model for highest quality wine

3. Visualize the optimal ranges of input parameters that produce high quality wine

Results

• The regression model had a Root Squared Mean Error (RSME) of 0.64 on a quality scale of 0-10 and a mean absolute percentage error (MAPE) of 0.08, which is a decent performance.

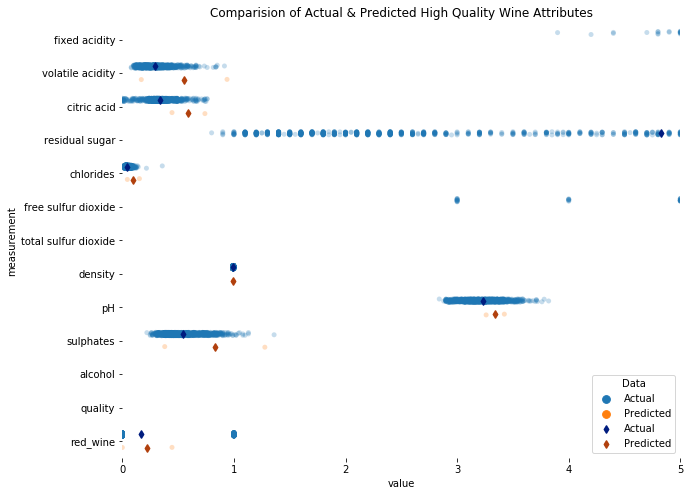Image showing close-up Comparison of Actual (blue) Predicted (red) High Quality Wine Attributes

• Most of the mean actual and predicted input attributes are pretty close, indicating that the model did a decent job of capturing its underlying data. There were wide ranges for some attributes like residual sugar, which show that high wine quality is not as sensitive these attributes. Attributes with narrow ranges, like chlorides, on the other hand, seemed to strongly affect wine quality.

Conclusion

We have implemented the SA optimization from scratch on a real-world dataset and found the optimal attributes that produce the highest quality Portuguese wine. As next steps, we could increase the number of temperature steps to verify earlier results. It would be awesome (perhaps with a similar or complementary dataset) to modify the cost function so that a small set of key wine characteristics are optimized and tailored to a specific consumer’s tastes.

This example illustrates the potential of applying SA to other problems, especially those with smaller and/or sparser datasets. This demonstrates that optimization techniques can be used on empirical datasets to find optimal ranges of input parameters based on a cost function. Alternative techniques include Bayesian optimization (can be used for model hyperparmeter optimization or for expensive cost function calls) and BFGS optimization algorithm (to find the best input parameters to a pre-trained deep neural network model).

The Code

Check out my simulated annealing optimization repo with the Python notebooks for access to the code.

```